

The final length of curve result is printed to the answer area along with the solution steps. The integral is evaluated, and that answer is rounded to the fourth decimal place. Then, that expression is plugged into the arc length formula. The CAS performs the differentiation to find dy⁄ dx. The routine calls on a JS computer algebra system (CAS) which can perform a derivative symbolically, maneuvering equations and applying derivative rules just like a person! When the "calculate" button is clicked, your inputted function and interval are read by the JS routine. The HTML creates the architecture of the calculator, the CSS provides the visual styling, and the JS provides all functionality and interactiveness. The Voovers Length of Curve Calculator is written in the web programming languages HTML (HyperText Markup Language), CSS (Cascading Style Sheets), and JS (JavaScript). In fact, the arc length formula is a simplified summation of an infinite number of distance formula evaluations for the straight lines. Each small change in x value is the dx from the arc length formula. The accuracy of that approximation gets better as we break the curve into a greater number of shorter straight lines.Īfter setting up the distance formula for the length of these line segments we may use an integral to make those line segments infinite in quantity and infinitesimally short. If each segment is treated as a straight line, we may use the distance formula to determine each line's length.Īdding up the lengths from these many straight lines gives an approximation of the curve's length.
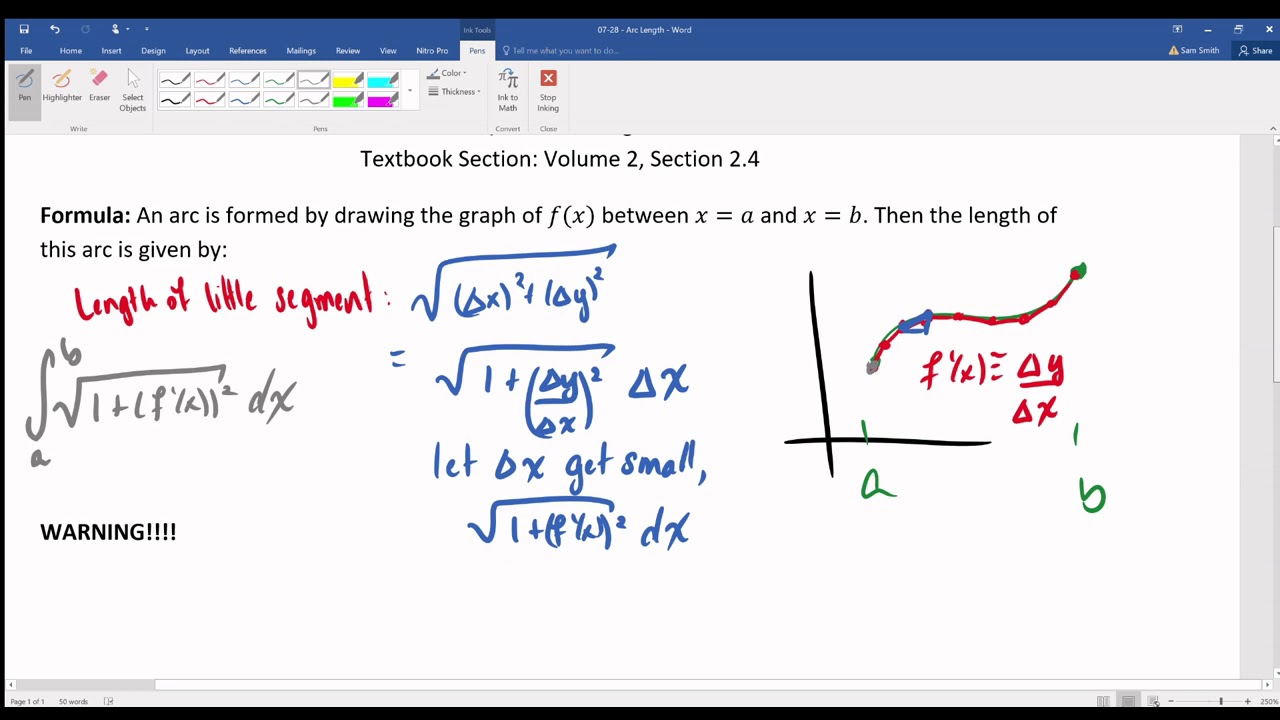
To approximate, we break a curve into many segments. The arc length formula is derived from the methodology of approximating the length of a curve. Where L is the length of the function y = f(x) on the x interval and dy/ dx is the derivative of the function y = f(x) with respect to x.
The formula for calculating the length of a curve is given as: This essentially boils down to finding the length of the curve (function), multiplying it by a constant and the function itself, and then integrating over the interval of interest to find the surface area.Īdditionally, by taking the coating's weight per unit area into account, we can then determine how much weight is added to our system when the coating is applied to the surface area of interest. If we are designing a bell shaped rocket nozzle that is parabolic in shape, we can take the function for the inner profile of the nozzle and revolve that profile around an axis to find the surface area of the nozzle's inner surface. Ablatives are commonly used on space vehicles and launch equipment to protect critical components under the resulting thermal loads seen during launch and flight. A substrate is the material that the coating is applied to. What if we are designing a rocket nozzle and want to find out how much ablative coating is required for the inside of this nozzle?Īn ablative coating protects a substrate that is exposed to high velocity, high temperature gases and particles for a finite amount of time. We can use this concept for more than just completing some math problems. Please e-mail any correspondence to Duane Kouba byĬlicking on the following address heartfelt "Thank you" goes to The MathJax Consortium and the online Desmos Grapher for making the construction of graphs and this webpage fun and easy.Why do we Learn About the Length of a Curve?įinding the length of a curve is another useful tool for our problem solving toolbox. Your comments and suggestions are welcome. Ĭlick HERE to see a detailed solution to problem 12.Ĭlick HERE to return to the original list of various types of calculus problems. $$ ARC = \displaystyle $ on the closed interval $ 1 \le y \le 2 $. It then follows that the total arc length $L$ from $x=a$ to $x=b$ is Using the Pythagorean Theorem we will assume that We will derive the arc length formula using the differential of arc length, $ ds $, a small change in arc length $s$, and write $ds$ in terms of $dx$, the differential of $x$, and $dy$, the differential of $y$ (See the graph below.). Consider a graph of a function of unknown length $L$ which can be represented as $ y=f(x) $ for $ a \le x \le b $ or $ x=g(y) $ for $ c \le y \le d $. Let's first begin by finding a general formula for computing arc length. The following problems involve the computation of arc length of differentiable functions on closed intervals. Arc Length of Differentiable Functions on a Closed IntervalĬOMPUTING THE ARC LENGTH OF A DIFFERENTIABLE FUNCTION ON A CLOSED INTERVAL


 0 kommentar(er)
0 kommentar(er)
